Aşa cum se ştie, ecuaţia de gradul 2 este scrisă sub forma: 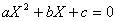 şi are soluţiile X₁ şi X₂, calculate prin formulele:

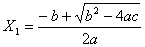 şi .
 

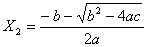          Astfel, pe panoul aplicaţiei se dispun trei elemente de control pentru datele de intrare numerice a, b şi c, două elemente indicatoare pentru datele de ieşire numerice reprezentand soluţiile ecuaţiei, X₁, X₂ şi un element indicator boleean de tip led pentru valoarea de sub radical pentru a semnala existenţa rădăcinilor reale, aşa cum se observă in Figura 1.

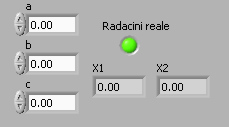
Fig. 1. Dispunerea elementelor de lucru pe panoul aplicaţiei

 

Etapele următoare sunt reprezentate de introducerea in diagramă a funcţiilor aritmetice şi logice necesare pentru calculul rădăcinilor X₁ şi X₂, in funcţie de valorile coeficienţilor a, b şi c. De asemenea, se definesc şi legăturile dintre componentele din diagramă pentru a stabili, astfel, fluxul de date al programului.

Pentru a calcula valoarea radicalului se utilizează operatorii matematici Multiply (inmulţire), Subtract (scădere), Compound Arithmetic şi Square Root (radical). Coeficientul b se conectează la ambele intrări ale operatorului Multiply, rezultatul fiind pătratul valorii sale iniţiale (b²). Coeficienţii a şi c, impreună cu o constantă de valoare 4 se conectează la Compound Arithmetic, setat pentru inmulţire cu trei intrări. Se face diferenţa b² - 4ac, obţinand o valoare Delta (Figura 2).

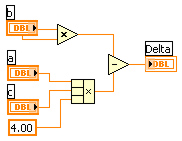
Fig. 2. Calculul valorii Delta, aflată sub radical

 

          Pentru a obţine rădăcini reale, valoarea Delta trebuie să fie mai mare sau egală cu zero, in caz contrar, rădăcinile sunt complexe. Această aplicaţie nu calculează rădăcinile complexe, dar avertizează, totuşi, utilizatorul in cazul in care nu mai obţine rădăcini reale. Avertizarea se realizează prin “aprinderea” ledului boolean, conectat, alături de funcţia radical, la valoarea Delta (Figura 3).

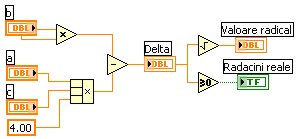
Fig. 3. Calculul radicalului şi stabilirea tipului soluţiilor (reale sau complexe)

 

          Pentru a calcula numărătorul fracţiilor ce dau valorile soluţiilor, coeficientul b trebuie să işi schimbe semnul (-b), prin intermediul operatorului Negate. In cazul soluţiei X₁, intre -b şi radical se va afla semnul plus (+), iar in cazul soluţiei X₂, intre –b şi radical se va afla semnul minus (-), aşa cum rezultă din Figura 4.

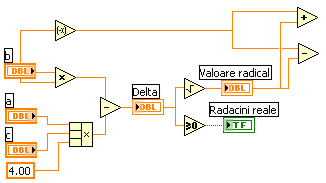
Fig. 4. Calculul numărătorilor fracţiilor pentru soluţiile X₁ şi X₂

 

Ambele fracţii au acelaşi numitor, valoarea calculată prin inmulţirea unei constante, 2, cu coeficientul a. Impărţind cei doi numărători la numitorul 2a se obţin soluţiile ecuaţiei de gradul doi. Astfel, diagrama finală este prezentată in Figura 5.

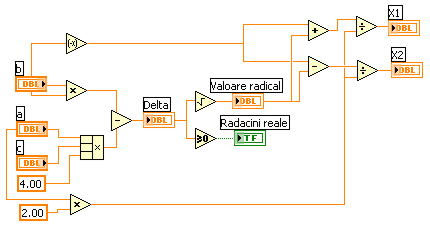
Fig. 5. Diagrama de rezolvare a ecuaţiei de gradul al doilea

 

Aplicaţia se rulează cu butonul [Run], dispus pe bara de instrumente a programului.